Subsets - 子集

Source

• lintcode: (17) Subsets

Given a set of distinct integers, return all possible subsets.

Note
Elements in a subset must be in non-descending order.

The solution set must not contain duplicate subsets.

Example
If S = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

题解

子集类问题类似Combination。

1. 首先对数组按升序排序
2. 回溯法递归

Java

class Solution {
    /**
     * @param S: A set of numbers.
     * @return: A list of lists. All valid subsets.
     */
    public ArrayList<ArrayList<Integer>> subsets(ArrayList<Integer> S) {

        ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
        if (S == null || S.size() == 0) {
            return result;
        }

        ArrayList<Integer> list = new ArrayList<Integer>();
        Collections.sort(S);
        backTrack(result, list, S, 0);
        return result;
    }

    private void backTrack(ArrayList<ArrayList<Integer>> result,
        ArrayList<Integer> list, ArrayList<Integer> num, int pos) {
        result.add(new ArrayList<Integer>(list));

        for (int i = pos; i < num.size(); i++) {
            list.add(num.get(i));
            backTrack(result, list, num, i + 1);
            list.remove(list.size() - 1);
        }
    }
}

Notice: backTrack(result, list, num, i + 1);中的『i + 1』不可误写为『pos + 1』，第一次写subsets的时候在这坑了很久... :(

回溯法可用图示和函数运行的堆栈图来理解，强烈建议使用图形和递归的思想分析，以数组[1, 2, 3]进行分析。下图所示为list及result动态变化的过程，箭头向下表示list.add及result.add操作，箭头向上表示list.remove操作。

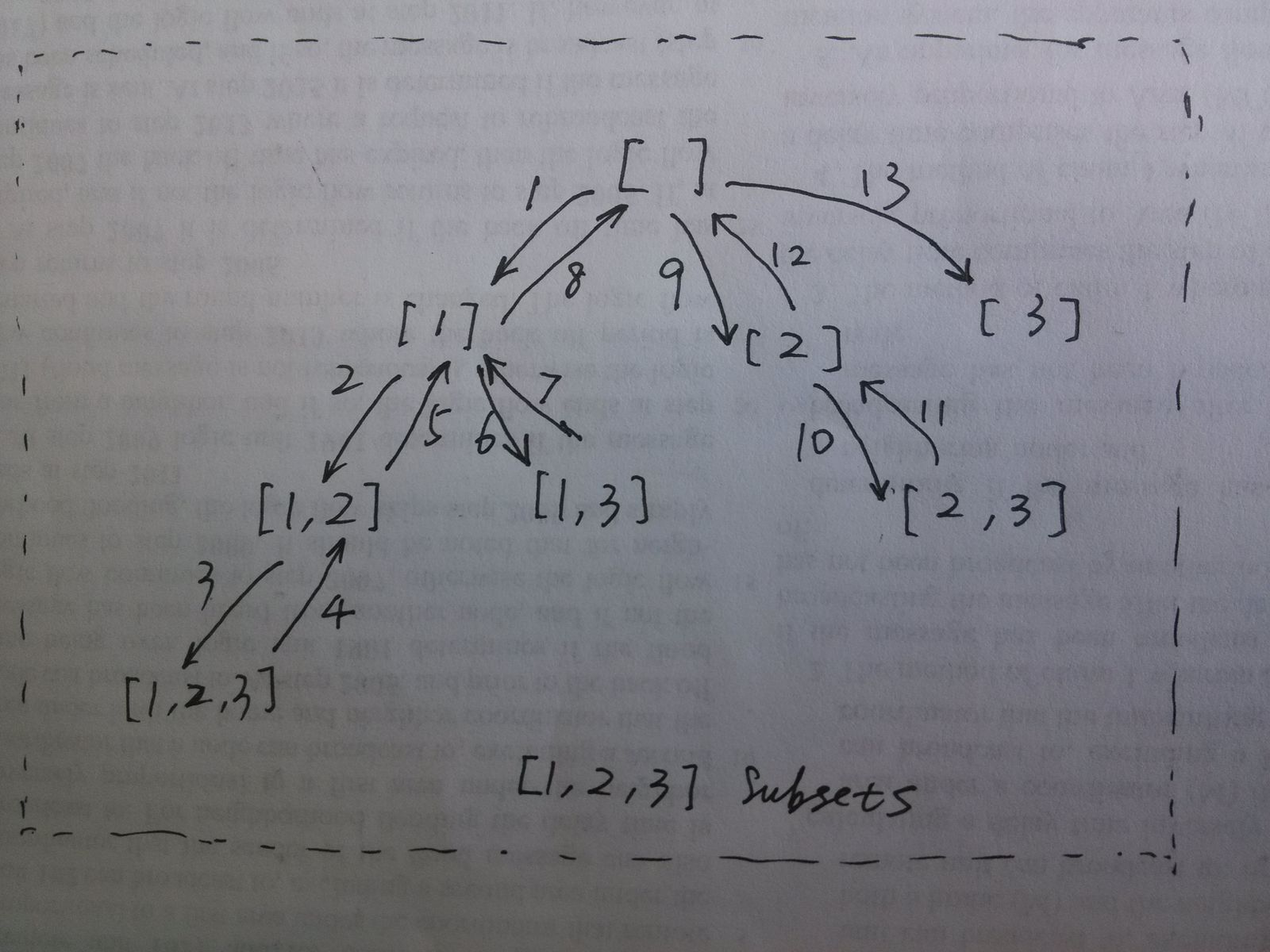
如果你不相信以上的图形化分析，还可以自己在纸上分析代码的调用关系，下面以数组[1,2]为例分析回溯法的调用栈。

1. 首先由主函数 subsets 进入，初始化 result 为[]，接着进行异常处理，随后初始化 list 为[]，递归调用backTrack(), num = [1, 2]。
2. result = [], list = [], pos = 0. 调用result.add()加入[], result = [[]]。进入for循环，num.size() = 2。
   • i = 0,
     1. list.add(num[0]) -> list = [1], 递归调用backTrack()前, result = [[]], list = [1], pos = 1
     2. 递归调用backTrack([[]], [1], [1, 2]，1)
        • result.add[[1]] -> result = [[], [1]]
        • i = 1, for(i = 1 < 2)
          1. list.add(num[1]) -> list = [1, 2]
          2. 递归调用backTrack([[], [1]], [1, 2], [1, 2]，2)
             • result.add[[1, 2]] -> result = [[], [1], [1, 2]]
             • i = 2 退出for循环，退出此次调用
          3. list.remove(2 - 1) -> list = [1]
          4. i++ -> i = 2
        • i = 2, 退出for循环，退出此次调用
     3. list.remove() -> list = []
     4. i++ -> i = 1，进入下一次循环
   • i = 1, for(i = 1 < 2)
     1. list.add(num[1]) -> list = [2]
     2. 递归调用backTrack([[], [1], [1, 2]], [2], [1, 2]，2)
        • result.add[[2]] -> result = [[], [1], [1, 2], [2]]
        • i = 2 退出for循环，退出此次调用
     3. list.remove(1 - 1) -> list = []
     4. i++ -> i = 2
   • i = 2, 退出for循环，退出此次调用
3. 返回结果result

C++

class Solution {
public:
    /**
     * @param S: A set of numbers.
     * @return: A list of lists. All valid subsets.
     */
    vector<vector<int> > subsets(vector<int> &nums) {
        vector<vector<int> > result;
        if (nums.empty()) {
            return result;
        }

        vector<int> list;
        backTrack(result, list, nums, 0);

        return result;
    }

private:
    void backTrack(vector<vector<int> > &result, vector<int> &list, \
                   vector<int> &nums, int pos) {
        result.push_back(list);

        for (int i = pos; i != nums.size(); ++i) {
            list.push_back(nums[i]);
            backTrack(result, list, nums, i + 1);
            list.pop_back();
        }
    }
};

Reference - 参考

• [NineChap 1.2] Permutation - Woodstock Blog
• 九章算法 - subsets模板
• LeetCode: Subsets 解题报告 - Yu's Garden - 博客园